[PyTorch] Softmax Classification 실습 : 모두를 위한 딥러닝 시즌2

Softmax 분류 이론 요약

 이전 포스팅에서는 sigmoid 함수로 H(x)를 계산하고, binary_cross_entropy 함수를 활용하여 Cost를 계산했다. 이 방법은 이진 분류 문제에 적합하다. 이번에는 다중 클래스 분류 문제에 적합한 방법을 알아보았다.

 

 간단하게 핵심을 정리하면 softmax 함수로 H(x)를 계산하고, cross_entropy 함수를 활용하여 Cost를 계산한다. softmax 함수는 여러 개의 실수로 이루어진 벡터를 확률 분포로 변환하며, cross_entropy 함수는 실제 레이블(one-hot 벡터)과 예측한 확률 분포의 차이를 구할 때 사용한다.

Softmax 분류 구현 코드

라이브러리 import & 시드값 고정

  

    
    
    
    
  
# Library import
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# For reproducibility
torch.manual_seed(1)

 

Softmax 함수 사용 예시

  

    
    
    
    
  
# Softmax function
z = torch.FloatTensor([1,2,3])
print(z)
hypothesis = F.softmax(z, dim=0)
print(hypothesis)
hypothesis.sum()

 

One-hot 벡터를 활용해서 직접 Cross Entropy Loss 계산

  

    
    
    
    
  
# Cross Entropy Loss (Low-level)
z = torch.rand(3, 5, requires_grad = True)
hypothesis = F.softmax(z, dim=1)
print(hypothesis)
y = torch.randint(5, (3,)).long()
print(y)

y_one_hot = torch.zeros_like(hypothesis)
print(y_one_hot.scatter_(1, y.unsqueeze(1), 1))

cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)

 

Log Softmax 연산 방법

1. softmax 함수와 log 함수

2. log_softmax 함수

  

    
    
    
    
  
# Cross-entropy Loss (torch.nn.functional)
# Low level
torch.log(F.softmax(z, dim=1))

  

    
    
    
    
  
# High level
F.log_softmax(z, dim=1)

 

Cross Entropy Loss 계산 방법

1. one-hot 벡터와 softmax 함수, log 함수

2. log_softmax 함수와 nll_loss 함수

3. cross_entropy 함수

  

    
    
    
    
  
# Low level
(y_one_hot * -torch.log(F.softmax(z, dim=1))).sum(dim=1).mean()

  

    
    
    
    
  
# High level (NLL: Negative Log Likelihood)
F.nll_loss(F.log_softmax(z, dim=1), y)

  

    
    
    
    
  
# F.cross_entropy = Combination of F.log_softmax and F.nll_loss
F.cross_entropy(z, y)

 

데이터 정의

  

    
    
    
    
  
# Data definition
x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)  # |x_train| = (m, 4)
y_train = torch.LongTensor(y_train)  # |y_train| = (m,)

 

훈련 진행

1. Low-level (one-hot 벡터, softmax 함수, log 함수)

2. Middle-level (cross_entropy 함수)

3. High-level (nn.Module 상속 → SoftmaxClassifierModel 클래스, cross_entropy 함수)

  

    
    
    
    
  
## 1. Training with Low-level Cross Entropy Loss
# Initialize model
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# Optimizer definition
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    
    # Calculate Cost
    hypothesis = F.softmax(x_train.matmul(W) + b, dim=1)
    y_one_hot = torch.zeros_like(hypothesis)
    y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
    cost = (y_one_hot * -torch.log(F.softmax(hypothesis, dim=1))).sum(dim=1).mean()
    
    # Gradient Descent
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # Log every 100 iterations
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

  

    
    
    
    
  
## 2. Training with F.cross_entropy
# Initialize model
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# Optimizer definition
optimizer = optim.SGD([W, b], lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    
    # Calculate Cost
    z = x_train.matmul(W) + b
    cost = F.cross_entropy(z, y_train)
    
    # Gradient Descent
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # Log every 100 iterations
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

  

    
    
    
    
  
## 3. High-level Implementation with nn.Module
# Softmax Classifier Class definition
class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(4, 3)  # Input: 4, Output: 3
        
    def forward(self, x):
        return self.linear(x)
    
model = SoftmaxClassifierModel()

# Optimizer definition
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    
    # Calculate H(x)
    prediction = model(x_train)
    
    # Calculate Cost
    cost = F.cross_entropy(prediction, y_train)
    
    # Gradient Descent
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # Log every 20 iterations
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

실행 결과 분석

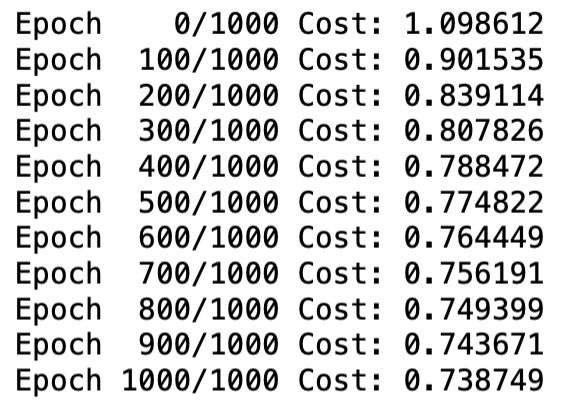
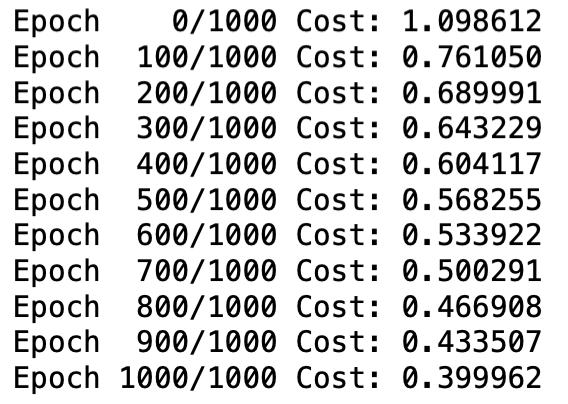
 같은 Epoch만큼 훈련을 시켰지만, High-level 방식으로 갈수록 Cost 감소량이 많다. 최종 Cost는 one-hot 벡터, softmax 함수, log 함수를 사용한 경우 약 0.739, cross_entropy 함수를 사용한 경우 약 0.400, nn.Module을 상속받고 cross_entropy 함수도 사용한 경우 약 0.242로 나타났다. 즉 고수준의 훈련 방식을 사용할수록 Cost가 작고 예측된 확률 분포가 실제 레이블에 가까워진다.

좌측에서부터 Low-level, Middle-level, High-level 방식 훈련의 결과

느낀 점

•  우선 Low level과 High level 훈련에서 얻은 최종 Cost 값의 차이가 커서 놀랐다. 가능하다면 nn.Module을 상속받아 사용하는 것이 좋으며, 기능이 압축된 cross_entropy 함수를 사용하는 편이 예측 정확도를 높이는 데 도움이 될 것 같다.
• one-hot 벡터를 생성하고 직접 cost를 계산하는 식은 복잡하지만, 이를 잘 이해해야 cross_entropy 함수를 의미 있게 사용할 수 있는 것 같다.
• 지난 포스팅부터 훈련 데이터의 형태와 H(x)와 Cost 계산 방식을 바꾸며 반복적으로 훈련 코드를 작성해 보니, 모델 훈련 단계에 점점 익숙해지는 것 같다. 

 

*참고 자료

모두를 위한 딥러닝 시즌2 - [PyTorch] Lab-06 Softmax Classification

https://youtu.be/B3gtAi-wlG8?feature=shared